पाइथागोरस थ्योरम क्या है | प्रमेय सूत्र | Top 7 Triplets Trick

आपको पता है पाइथागोरस थ्योरम क्या है ? हम पाइथागोरस थ्योरम की मदद से गणित के बड़ी से बड़ी सवाल को चुटकियों में हल कर सकते हैं। इसको जानना आपके लिए आज के समय में बहुत जरुरी है। हम इस आर्टिकल में इनके सूत्र को देखेंगे और इनको सिद्ध भी करेंगे। आप पाइथागोरस त्रिक की माध्यम से कैसे बड़ी-बड़ी सवाल को सेकंडों में हल कर सकते हैं ये भी देखेंगे। ये जानकरी आपको क्लास 5th, 6th या फिर 10th क्लास या कहें 12th क्लास में ही नहीं Competition के सवाल को हल करने में भी मदद करेगा। इस लेख में पढ़ें पूरी जानकारी दिया हूँ ।

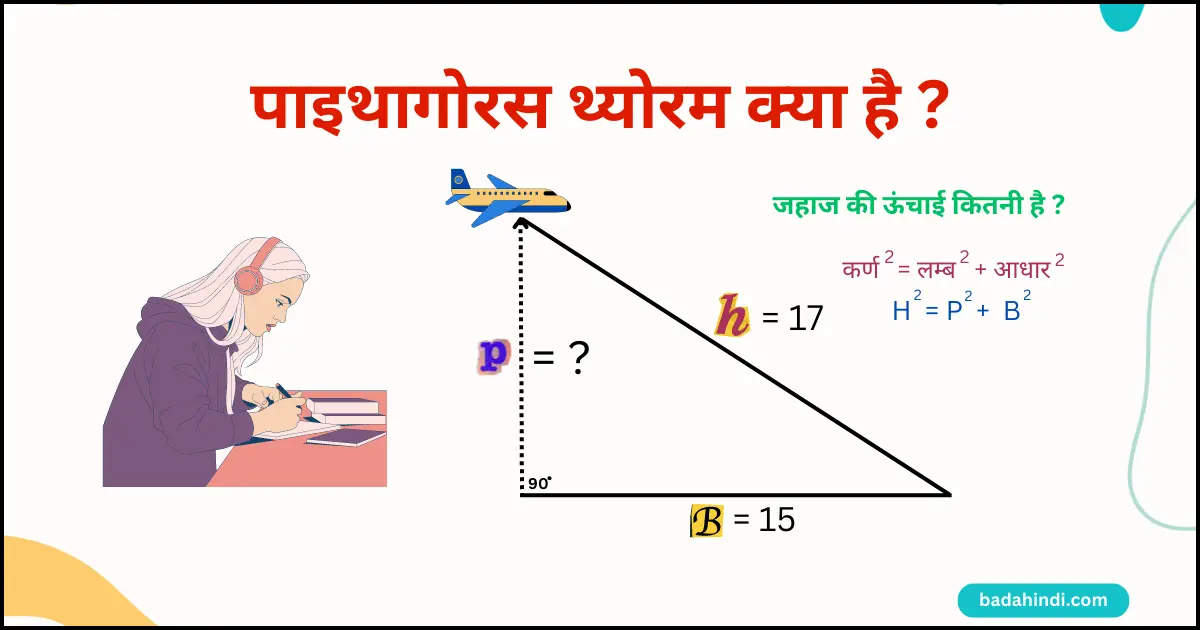
पाइथागोरस थ्योरम क्या है

ये पाइथागोरस थ्योरम मैथ का एक ऐसा फार्मूला या कहें विधि है जिसका उपयोग कई जगह काम में आता है। आप ज्योमेट्री की बात कर ले वहां पाइथागोरस थ्योरम का यूज है। आप ट्रिग्नोमेट्री की बात कर ले वहां इसका यूज होता है। अगर आपको किन्ही दो पॉइंट की की बीच की दूरी पता करना है वहां पाइथागोरस थ्योरम का यूज़ होता है या फिर किसी चीज का हाइट पता करना है तब वहां हम पाइथागोरस थ्योरम का युद्ध करते हैं। तो इसका कई जगह यूज़ होता है। इसी कारण से पाइथागोरस थ्योरम का अच्छी से अंडरस्टैंडिंग होना जरुरी है।

 

समकोण त्रिभुज कैसे पहचाने ?

अब जैसे मान लीजिए मेरे पास एक राइट एंगल ट्रायंगल है, मतलब उस त्रिभुज की तीन एंगल में से किसी एक एंगल 90° का है। तो वो एक Right Angle है, जिसको हम समकोण त्रिभुज बोलते हैं।

अब पाइथागोरस थ्योरम की मदद से उस त्रिभुज के कोई दो भुजा (Side) का मान दिया हो, तो मैं तीसरे भुजा (Side) का पता लगा सकता हूं। अब यह देखने से पहले यह कैसा होता है एक और छोटी सी चीज है। वह यह देखना है कि राइट एंगल ट्रायंगल में से एक कोण 90 डिग्री का होगा। उस कोण का अपोजिट साइड उस त्रिभुज का सबसे लंबा साइड या भुजा होगा और इस लंबा साइट को हाइपोटेनियस (कर्ण) बोलेंगे।

यहां पर यह जरूरी है अगर कोई भी Right Angle Triangle हो तो आराम से देख कर यह पता लगा सके कि उस Triangle का कर्ण (Hypotenious) कौन सा है।

मान लीजिए मेरे पास एक ऐसा त्रिभुज (Triangle) है। अगर मैं आपको बोलूं कि इसमें hypotenious कौन सी साइड होगी तो यहां मैं देख कर बता सकता हूं कि 90° के ऑपोजिट साइड वाला कर्ण (Hypotenious) होगी।

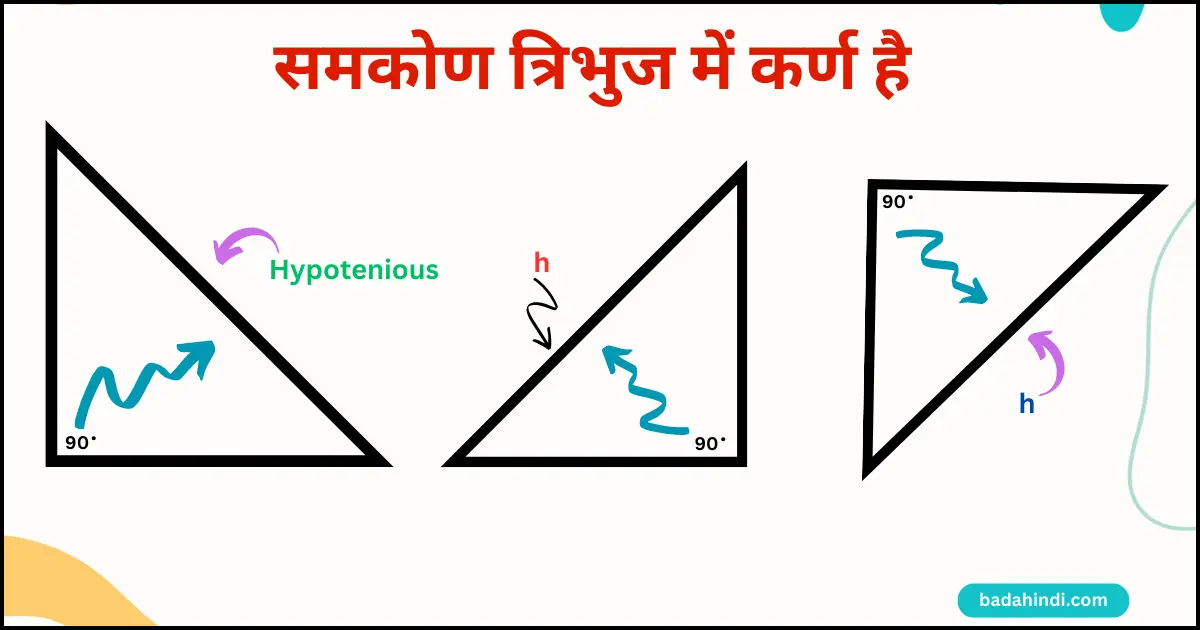
ऊपर चित्र में हमने इसी तरह से कुछ और उदाहरण लिए हैं जिससे यह क्लियर हो जाए कि Hypotenious पहचानना हमें अच्छी तरह से आ गया है।

 

पाइथागोरस सिद्धांत क्या है ?

इसका सिंद्धांत महान यूनानी गणितज्ञ पाइथागोरस ने दिया था इसे ही पाइथागोरस प्रमेय का जनक कहा जाता है। पाइथागोरस हमें यह बताता है की एक समकोण त्रिभुज का कर्ण का वर्ग दो अन्य भुजा के वर्ग के बराबर होता है, यही पाइथागोरस का सिद्धांत कहता है। इनको और डिटैल में समझते हैं पढ़ें आगे।

 

पाइथागोरस प्रमेय का सूत्र

आइए अब देखते हैं :

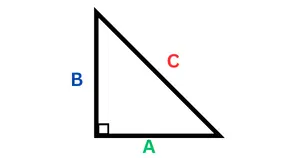
मान लीजिए एक Right Angle Triangle दिया हुआ है। इसमें कुछ भुजा  इस प्रकार से दिया हुआ है A, B, और C भुजा ।

यहां पाइथागोरस थ्योरम हमसे कहता है कि त्रिभुज के दो छोटे साइड के स्क्वायर का योग बराबर होगा, उस त्रिभुज के बड़े वाले साइड के स्क्वायर के बराबर यानी कि

•   A² + B² = C²

∴       आधार² + लम्ब² = कर्ण²

• यह हमें पाइथागोरस थ्योरम बताता है। इसे ही पाइथागोरस प्रमेय सूत्र भी कहते हैं।

 

पाइथागोरस प्रमेय सिद्ध करें

किसी भी समकोण त्रिभुज के कर्ण का वर्ग शेष दो भुजाओं के वर्गों के योग के बराबर होता है ।

यानि की,

कर्ण² = लम्ब² + आधार²

 

प्रमेय 6.8 (पाइथागोरस प्रमेय)

कथन : एक समकोण त्रिभुज में कर्ण का वर्ग शेष दो भुजाओं के वर्गों के योग के बराबर होता है ।

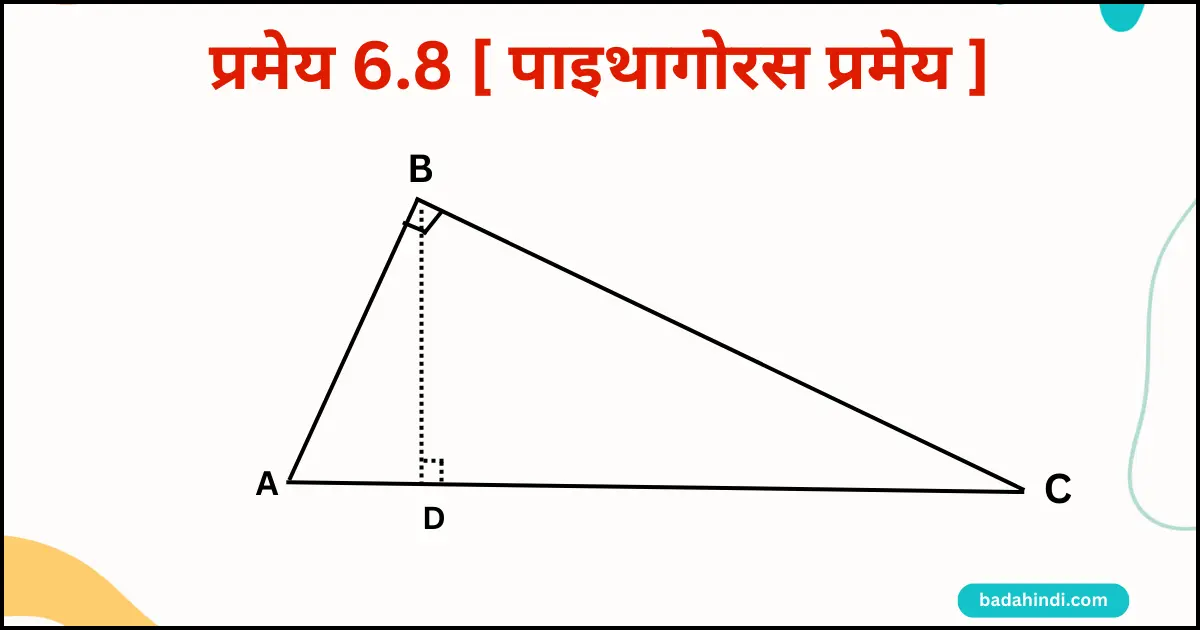
नोट: यहाँ ध्यान देना इस त्रिभुज में तीन त्रिभुज बना है। दो छोटे और एक बड़े वाला त्रिभुज तो हमें दोनों छोटे त्रिभुज को बारी-बारी से बड़े वाले के साथ तुलना करेंगे तो आसानी से सिद्ध हो जायेगा।

दिया है:

• ABC एक समकोण त्रिभुज है, जिसमें
• ∠B = 90°      —  (i)

रचना,

त्रिभुज के शीर्ष B से भुजा AC पर लम्ब BD डाला । इसलिए AD+DC= AC बना है।

अतः  ∠D = 90° बना   — (ii)

हमें सिद्ध करना है,

AC² = AB² + BC²

Δ ABD व Δ ABC में,

∠A = ∠A  (उभयनिष्ठ कोण है)

∠B = ∠D = 90 (समीकरण (i) और (ii) से)

अतः कोण-कोण समरूपता कसौटी से,

ΔABD ∼ ΔABC  है ।

अतः संगत भुजाओं का अनुपात बराबर होगा ।

AB/AC = AD/AB

⇒     (AB)² = (AC) × (AD)  — (iii)

अब,

ΔBDC व ΔABC में,

∠C = ∠C (उभयनिष्ठ कोण)

∠B = ∠D = 90°   (समीकरण (i) व (ii) से)

अतः कोण-कोण समरूपता कसौटी से,

ΔBDC ∼ ΔABC  है ।

अतः संगत भुजाओं का अनुपात समान होगा ।

BC/AC = DC/BC

⇒     (BC)² = (AC) × (DC)  — (iv)

समीकरण (iii) और (iv) से,

(AB)² + (BC)² = (AC × AD) + (AC × DC)    (ध्यान देना यहाँ पे हमने समीकरण (iii) और (iv) को जोड़ दिया है)

⇒      (AB)² + (BC)² = AC × (AD+DC)   ( चूँकि AC दोनों में Comman है इसलिए एक को निकल दिए)

⇒       (AB)² + (BC) = (AC × AC)   (चूँकि AC = AD +DC है)

∴       (AB)² + (BC)² = (AC)²    Verified.

 

प्रमेय 6.9 (पाइथागोरस प्रमेय का विलोम)

कथन: यदि किसी त्रिभुज की एक भुजा का वर्ग अन्य दो भुजाओं के वर्गों के योग के बराबर हो, तो पहली भुजा का सम्मुख कोण समकोण होता है ।

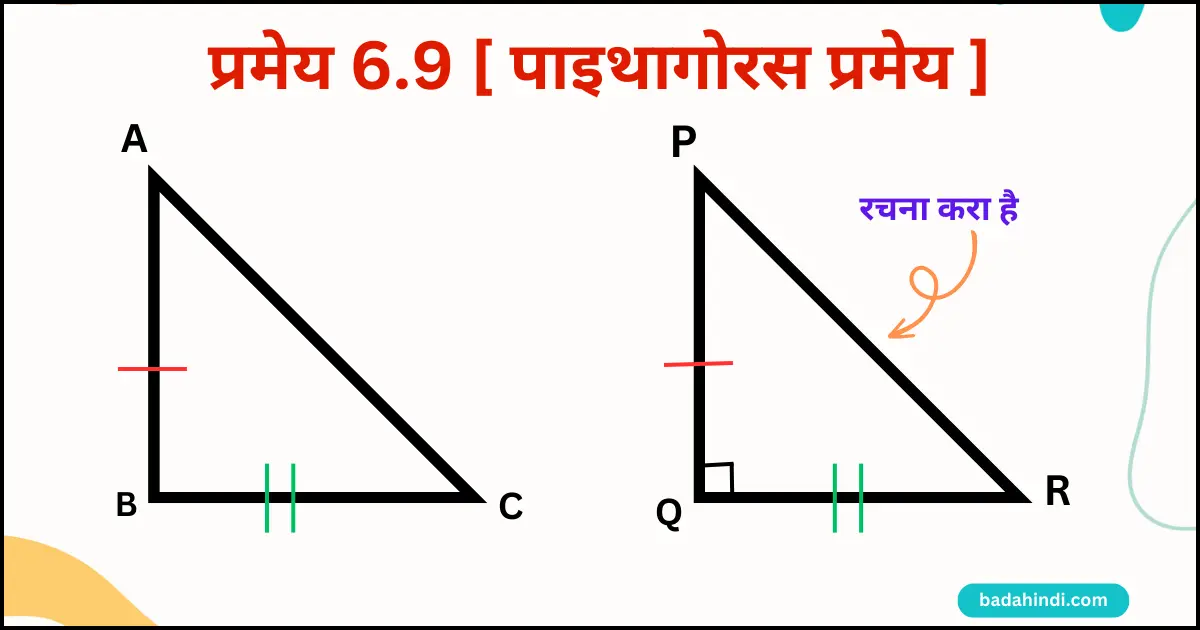
दिया है,

AC² = AB² + BC²  —  (i)

सिद्ध करना है,

∠B = 90°   या ΔABC एक समकोण त्रिभुज है ।

 

रचना,

ΔPQR एक समकोण Δ बनाया जिसमें

∠Q = 90° —  (ii)

तथा   AB = PQ  —  (iii)

एवं    BC = QR  —  (iv)

 

ΔPQR में,

∠Q = 90°

अतः पाइथागोरस प्रमेय से,

PR² = PQ² + QR²

⇒     PR² = (AB)² + (BC)²   —  (v)

समीकरण (i) का मान समीकरण (v) में रखने पर,

PR² = AC²

⇒      PR = AC    —  (vi)

समीकरण (iii), (iv) व (vi) से,

ΔABC ≅ ΔPQR    (भुजा-भुजा-भुजा सार्वंगसम  प्रमेय से)

अतः संगत कोण समान होंगे,

∴      ∠B = ∠Q

अतः  ∠B = 90°    {समीकरण (ii) से}

∴      ΔABC एक समकोण त्रिभुज है।

Verified.

 

पाइथागोरस प्रमेय के सवाल

अब आप ये जान गए कि पाइथागोरस थ्योरम क्या है तो अब हम इसी को हम एग्जांपल के द्वारा देखते हैं ताकि यह चीज हमारे दिमाग में बैठ जाए।

मान लेते हैं जैसे कि हमारे पास राइट एंगल ट्रायंगल दिया हुआ है। यहां पर दो Side दिया हुआ है। एक 3cm है और दूसरा 4cm है तो हमें तीसरे साइड का निकालना है तो हम कैसे निकालेंगे। तो हम यहां यूज करेंगे पाइथागोरस थ्योरम का ।

इस त्रिभुज (Triangle) में पाइथागोरस लगाने से पहले हमें यह फाइंड करना होता है कि इस त्रिभुज का राइट एंगल ट्रायंगल में हाइपोटेनियस कौन वाला है। तो हमने पहले ही सीख लिया है कि कैसे फाइंड करना है। तो यहां देखते हैं।

 

प्रश्न 1. इस त्रिभुज का कर्ण क्या होगा ?

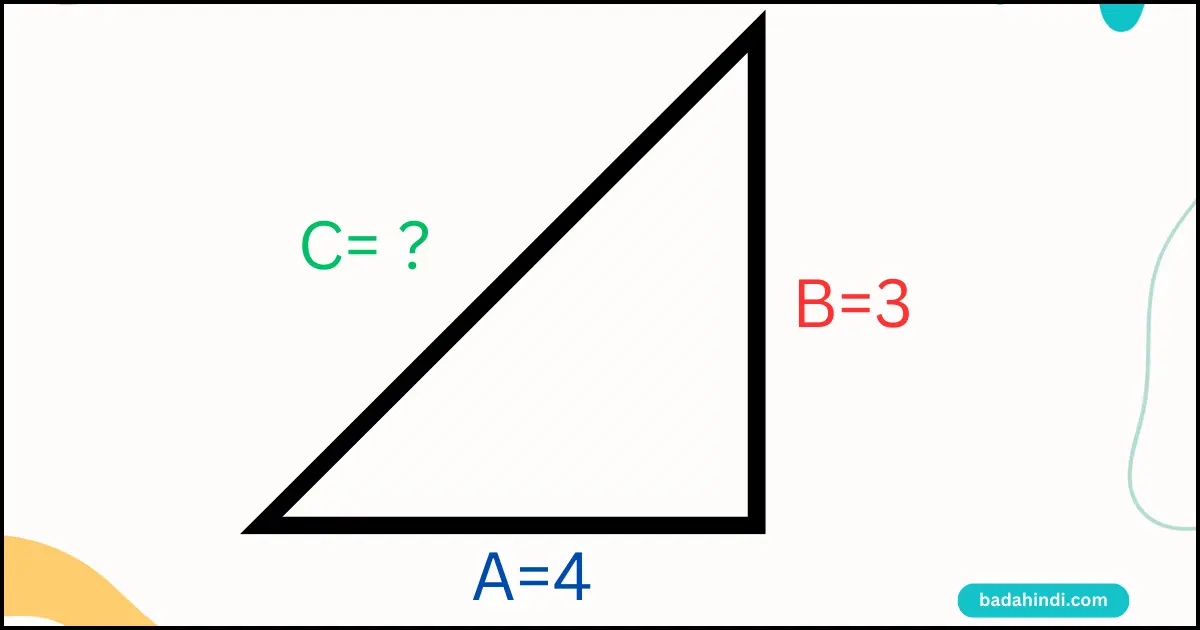
एक त्रिभुज में 90 डिग्री है। तो इसी के ऑपोजिट हाइपोटेनियस (कर्ण) होगा और Hypotenious ही त्रिभुज की सबसे बड़ी भुजा होती है। तो अब हम यहां पर पाइथागोरस थ्योरम का यूज कर सकते हैं।

पाइथागोरस थ्योरम

A² + B² = C²   इस सूत्र में हम त्रिभुज का मान को रखेंगे ।

⇒     A=3, B= 4 है।

हमें   C = ?  का निकलना है ।

इसलिए,

A² + B² = C²     (यानि आधार² + लम्ब² = कर्ण²)

∴      4² + 3² = C²     (यहाँ हमने मान बैठा दिया)

⇒     16 + 9 = C²

⇒     25 = C²

∴     C = √25  ( यहाँ पे हम C का root को दाएं साइड ले गए तो Under  Root हो गया।

⇒     C = 5  ( यानि की Δ की तीसरा भुजा 5 होगा। )

आप यहाँ पर Δ की तीनों भुजा को देख सकते हैं ।

यहाँ पर यह सिद्ध हो जाता है की Hypotenious ही Δ की सबसे बड़ी साइड होती है ।

 

प्रश्न 2. त्रिभुज का आधार कितना होगा ?

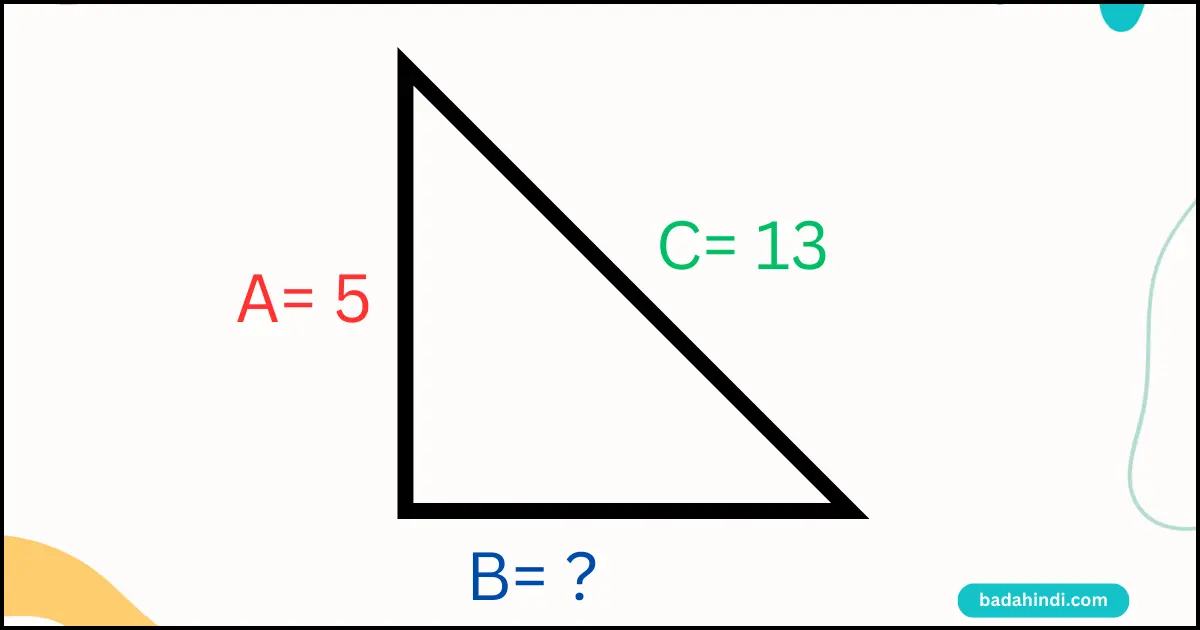
दिया है,

• a = 5
• b = ?
• c = 13

हल:

पाइथागोरस प्रमेय से,

 A² + B² = C²

or,     5² + B² = 13²

⇒      25 + B² = 169

⇒      B² = 169 – 25

or,     B = √144

or,     B = 12

अतः त्रिभुज का आधार 12 होगा।

आपने बेसिक तरीका सिख लिया की कैसे तीसरा भुजा निकला जाता है । अब आप एडवांस्ड तरीका सीखें भुजा निकालने के लिए।

 

यह भी देखें :

• भूकंप क्या है  

 

पाइथागोरस त्रिक (Pythagorean Triplets)

आप Triplets की मदद से बड़े से बड़े Maths के सवाल को हल कर सकते हैं। आपको सिर्फ Tripletes के कुछ सीरीज को याद करके रखना है, उन्हीं के मदद से बनाएंगे। यदि आप इसको 4-5 बार बनाएंगे तो ऑटोमेटिक आपके दिमाग में बैठ जायेगा।

निचे कुछ महत्त्वपूर्ण Triplets सीरीज दिए हुए हैं :

• सीरीज :
  • 3, 4, 5
  • 5, 12, 13
  • 7, 24, 25
  • 8, 15, 17
  • 6, 8, 10
  • 9, 40, 41
  • 11, 60, 61

हम पहला सीरीज को लेते हैं :

• 3, 4, 5

इससे किस प्रकार सवाल बन सकते हैं। आपको देखना है इनसे कितना गुना ज्यादा है। जैसे :

3, 4, 5 6, 8, 10 9, 12, 15 12, 16, 20 15, 20, 25

• यहाँ हमने 3×2=6, 4×2=8 और 5×2=10 करके आगे लिखे हैं ।

सवाल है : इस त्रिभुज का लम्ब कितना होगा ?

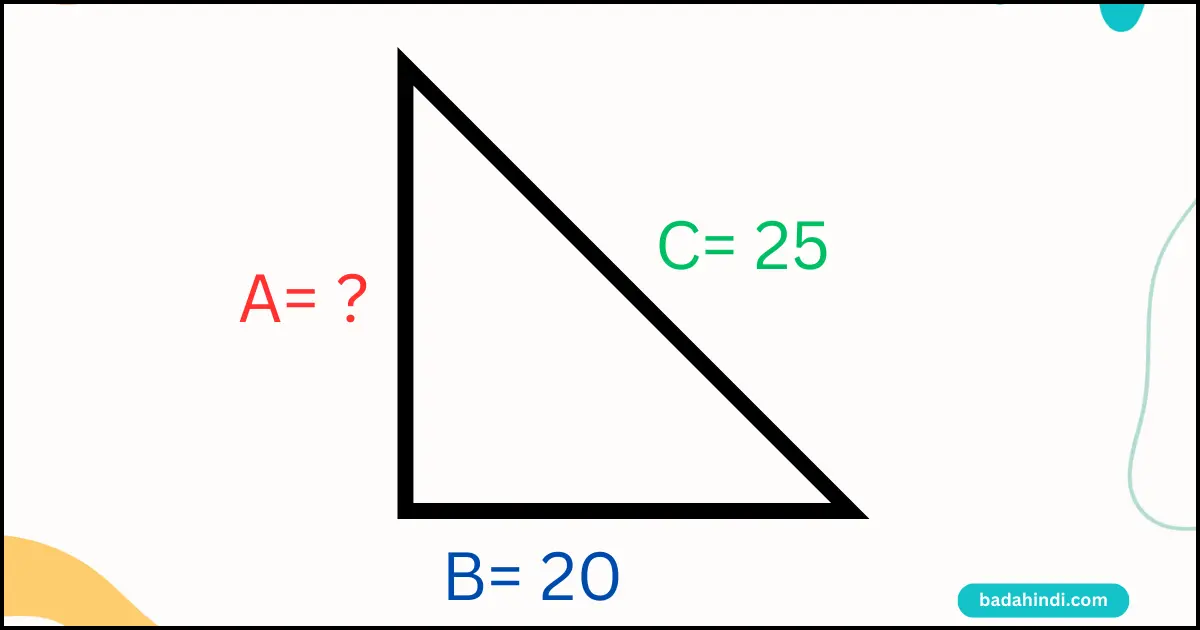
क्या आप, इसको बेसिक विधि से बनाएंगे। नहीं यहाँ पर हमें Triplets विधि का Use करना है। ऊपर में आपको कुछ सीरीज याद करने के लिए दिए हैं उनमें से सबसे पहले 3, 4 और 5, से गुना करके देखेंगे ।

जैसे : कर्ण, 5 ×5 = 25 और आधार, 4 × 5 = 20 तो लम्ब, 3 × 5 = 15 होगा ।

आगे इसी तरह से आप Triplet का उपयोग करके देखें कौन वाला हो सकता है ।

इस तरह करके आप बना सकते हैं ।

 

पाइथागोरस प्रमेय किस त्रिभुज से संबंधित है ?

हमने यहाँ पाइथागोरस प्रमेय का उपयोग समकोण त्रिभुज में उपयोग किया है। यह त्रिभुज के बिच सम्बन्ध को बताता है। पर ऐसा बिलकुल भी नहीं है। पाइथागोरस को उपयोग की जगह में होता है। इसकी मदद से हम कोई भी दुरी को भी निकल सकते हैं । पहाड़ों की ऊंचाई, पेड़ों की, हवाई जहाज की और भी उनके क्षेत्रों में इसका उपयोग है ।

 

यह भी पढ़ें :

• हमारे सौरमंडल के सभी 8 ग्रहों की जानकरी

 

निष्कर्ष

इस आर्टिकल में हमने देखा पाइथागोरस थ्योरम क्या है ? पाइथागोरस का सिद्धांत,  पाइथागोरस त्रिक से संबंधित सवाल और इनको सिद्ध भी किये। समकोण त्रिभुज कैसे पहचने की पाइथागोरस त्रिक का उपयोग करें । इन सब टॉपिक को हमने यहाँ देखा आपको ये जानकरी कैसे लगा जरूर बताएं। और भी अच्छे-अच्छे जानकारी के लिए जुड़े रहें । धन्यवाद !

 

FAQs

Q1. पाइथागोरस प्रमेय क्या है समझाइए?

उत्तर- पाइथागोरस थ्योरम क्या है? पाइथागोरस थ्योरम के अनुसार समकोण त्रिभुज के कर्ण का वर्ग अन्य दो भुजाओं के वर्गों के बराबर होता है । जैसे : कर्ण² = लम्ब² + आधार² ।

 

Q2. पाइथागोरस प्रमेय का जनक कौन है?

उत्तर- पाइथागोरस के जनक यूनानी दार्शनिक पाइथागोरस को मन जाता है।

 

Q3. पाइथागोरस प्रमेय का सूत्र क्या है ?

उत्तर- कर्ण² = लम्ब² + आधार²